Laporan Praktikum Larik Dan Matrik 2
www.hajarfisika.com
Laporan Praktikum Larik dan Matrik 2







3. Gabungan Larik



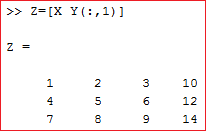


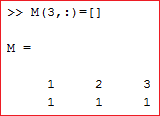












Laporan Praktikum Larik dan Matrik 2
Larik dan Matrik 2
1. Mengambil sebagian Elemen

Matriks A didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

Matriks B didefinisikan dengan mengambil nilai matriks A pada baris 2 hingga 3 dan kolom 1 hingga 3

Matriks B dIdefinisikan lagi dengan mengambil nilai matriks A pada baris 1 untuk semua nilai dikolom itu
Berdasarkan percobaan tersebut, fungsi :
- Simbol ':' : untuk mengambil semua elemen baris atau kolom pada matriks

Matriks B dedefinisikan lagi dengan mengambil nilai matriks A pada baris 2 hingga 3 untuk semua nilai dikolom itu
2. Menukar kolom/baris

Matriks A didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

- Matriks B didefinisikan dengan menukar nilai matriks A pada baris 1 dengan baris 2 untuk semua nilai dikolom itu
- Nilai -1 dipakai untuk menukar suatu baris atau kolom
- Ditambahkan juga A(3,:) pada baris selanjutnya sebab kalau hanya mendefinisikan A(2:-1:1,:) maka hanya akan terbaca 2 baris saja pada matriks A
- Untuk penambahan nilai baris pada matriks cukup diberi simbol ';' saja dengan tutup kurung siku pada fungsi nya '[ ]'

- Matriks B didefinisikan dengan menukar nilai matriks A pada kolom 1 dengan kolom 3 untuk semua nilai dibaris itu
- Ditambahkan juga A(:,4) pada kolom selanjutnya sebab kalau hanya mendefinisikan A(:,3:-1:1) maka hanya akan terbaca 3 kolom saja pada matriks A
- Untuk penambahan nilai kolom pada matriks cukup diberi spasi saja dengan tutup kurung siku pada fungsi nya '[ ]'
3. Gabungan Larik

Matriks X dan Y didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

- Matriks Z didefinisikan dengan menggabungkan nilai matriks X dan Y.
- Untuk penggabungannya cukup memberi spasi saja dengan tutup kurung siku pada fungsinya '[ ]'

- Matriks Z didefinisikan lagi dengan menggabungkan nilai matriks X dan Y untuk semua nilai X dan sebagian nilai Y (semua nilai kolom pada baris ke 1)
- Tetapi kesudahannya akan mengalami error (tidak sanggup digabungkan) sebab pengambilan sebagian matriks Y mempunyai jumlah baris yang tidak sama dengan matriks X
- Untuk pengambilan elemen tertentu pada matriks cukup diberi tanda kurung '( )' dan diisikan baris dan kolom yang mau diambil
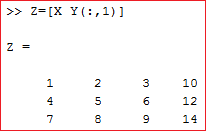
- Matriks Z didefinisikan lagi dengan menggabungkan nilai matriks X dan Y untuk semua nilai X dan sebagian nilai Y (semua nilai baris pada kolom ke 1)
- Hasil ini tidak error ibarat percobaan yang sebelumnya sebab pengambilan sebagian matriks Y mempunyai jumlah baris yang sama dengan matriks X
4. Mengubah elemen matrik jadi array

- Matriks K didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas
- Matriks K lalu diubah menjadi array (hanya mempunyai 1 kolom) dengan urutan dari kolom 1 pada baris 1 hingga 3, kolom 2 pada baris 1 hingga 3, dan seterusnya. Hasilnya ibarat gambar diatas sebelah kanan
- Untuk pengubahan matriks menjadi array ini memakai tanda '(:)' pada matriks yang mau diubah menjadi array
5. Perkecil Matriks

Matriks M didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas
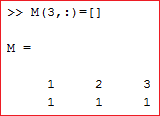
- Matriks M diperkecil dengan menghilangkan semua kolom pada baris 3
- Untuk memperkecil matriks atau menghilangan baris/kolom pada matriks cukup diberi tanda kurung '( )' lalu diisikan baris dan kolom yang mau dihilangkan
- Pada tanda '[ ]' tidak diisi apapun, mengatakan pembatalan baris dan kolom pada matriks
6. Ganti isi matrik dengan vektor/array

Matriks S didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

Array t didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

- Array t lalu menggantikan nilai semua kolom pada baris 2 dengan algoritma ibarat gambar diatas
- Untuk menggantikan isi matriks dengan array cukup diberi tanda kurung '( )' lalu diisikan baris dan kolom yang mau digantikan dengan array t
7. Ganti isi matrik dengan nilai yang sama

Matriks S didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

- Nilai 10 lalu menggantikan baris 1 hingga 3 pada kolom 2
- Untuk menggantikan isi matriks dengan suatu nilai cukup diberi tanda kurung '( )' lalu diisikan baris dan kolom yang mau digantikan dengan nilai tersebut
8. Fungsi larik

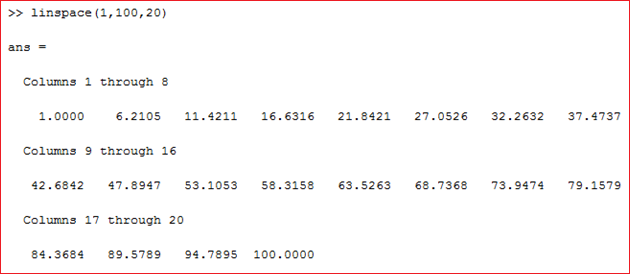
- linspace (linearly spaced vector) yakni jarak antar vektor yang secara linier
- linspace dibentuk dengan nilai awal 1, nilai simpulan 100, sebanyak 20 buah dan kesudahannya didapatkan ibarat gambar diatas
- Rentang pada linspace ditentukan oleh kegiatan itu sendiri dengan rentang yang sama dari nilai awal hingga nilai akhir

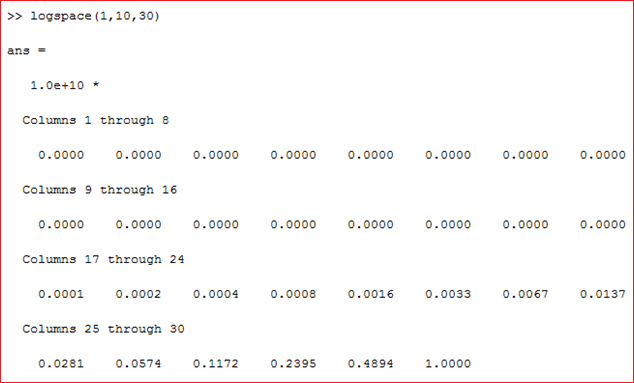
- logspace (logarithmically spaced vector) yakni jarak antar vektor yang secara logaritmik
- logspace dibentuk dengan nilai awal 1, nilai simpulan 10, sebanyak 30 buah dan kesudahannya didapatkan ibarat gambar diatas
- Berarti perhitungan di mulai dari 101 hingga 1010 sebanyak 30 buah
- Sama ibarat linspace, rentang pada logspace juga ditentukan oleh kegiatan itu sendiri dengan rentang yang sama dari nilai awal hingga nilai akhir

Untuk mempermudah analisa maka hasil diatas sanggup ditulis juga sebagai :
1. 1010 x 10-9 = 10
2. 1010 x (2.043360 x 10-9) = 20.4336
3. 1010 x (4.175319 x 10-9) = 41.75319
.
.
.
28. 1010 x (2.39502661998748 x 10-1) = 2 395 026 619.98 748
29. 1010 x (4.89390091847750 x 10-1) = 4 893 900 918.47 750
30. 1010 x 1 = 1010 = 10 000 000 000
9. Ukuran Matriks

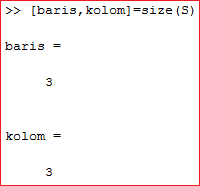
Matriks S didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

Untuk menampilkan gosip ukuran matriks sanggup dipakai algoritma ibarat gambar diatas yaitu size(S) dengan S yakni matriks yang ingin diketahui ukurannya

Dapat juga diberi display baris dan kolom memakai algoritma diatas

Jika ingin menampilkan ukuran barisnya saja atau kolomnya saja sanggup memakai algoritma ;
- baris=size(S,1) untuk ukuran barisnya
- kolom=size(S,2) untuk ukuran kolomnya
10. Pencarian Posisi

Matriks A didefinisikan terlebih dahulu pada Command Window dan kesudahannya ibarat gambar diatas

Untuk mencari data yang tidak nol pada matriks A sanggup dipakai algoritma ibarat gambar diatas, dan kesudahannya ditampilkan dalam indeks baris dan kolom

Untuk mencari data dengan kriteria tertentu, misal cari posisi angka 2 sanggup dipakai algorimta ibarat gambar diatas, dan kesudahannya akan ditampilkan dalam indeks baris dan kolom
Belum ada Komentar untuk "Laporan Praktikum Larik Dan Matrik 2"
Posting Komentar