Laporan Praktikum Larik Dan Matrik 3
www.hajarfisika.com
Laporan Praktikum Larik dan Matrik 3
1. Any









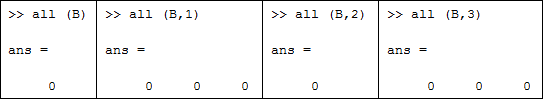














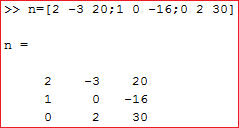









Laporan Praktikum Larik dan Matrik 3
Larik dan Matrik 3
1. Any

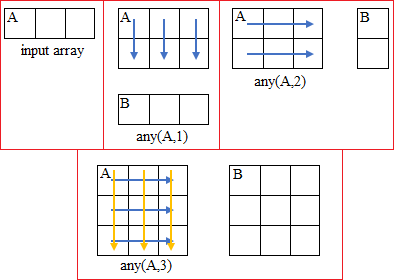
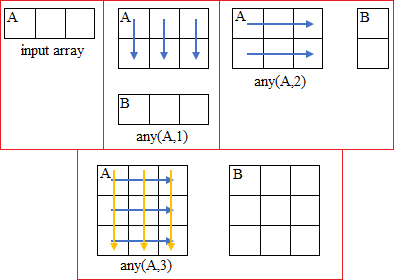
Larik A didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi any dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- any (A) = 1, menunjukkan beberapa dari elemen larik A baris 1 kolom 1, kolom 2, dan kolom 3 ialah bernilai benar (1) atau tidak salah (0)
- any (A,1) = 0 1 1, menunjukkan beberapa dari elemen larik A kolom 1 bernilai salah (0), kolom 2 dan kolom 3 bernilai benar (1)
- any (A,2) = 1, menunjukkan beberapa dari elemen larik A baris 1 bernilai benar (1)
- any (A,3) = 0 1 1, menunjukkan beberapa dari elemen larik A kolom 1 bernilai salah (0), kolom 2 dan kolom 3 bernilai benar (1)

Larik B didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi any dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- any (B) = 0, menunjukkan beberapa dari elemen larik B baris 1 kolom 1, kolom 2, dan kolom 3 ialah bernilai salah (0) atau tidak benar (1)
- any (B,1) = 0 0 0, menunjukkan beberapa dari elemen larik B baris 1 kolom 1, kolom 2, dan kolom 3 bernilai salah (0)
- any (B,2) = 0, menunjukkan beberapa dari elemen larik B baris 1 bernilai salah (0)
- any (B,3) = 0 0 0, menunjukkan beberapa dari elemen larik B baris 1 kolom 1, kolom 2, dan kolom 3 bernilai salah (0)

Larik C didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi any dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- any (C) = 1 1 1, menunjukkan beberapa dari elemen matriks C kolom 1, kolom 2, dan kolom 3 bernilai benar (1) pada seluruh baris
- any (C,1) = 1 1 1, menunjukkan beberapa dari elemen matriks C kolom 1, kolom 2, dan kolom 3 bernilai benar (1) pada seluruh baris
- any (C,2) = 1 ; 1 ; 1, menunjukkan beberapa dari elemen matriks C baris 1, baris 2, dan baris 3 bernilai benar (1) pada seluruh kolom
- any (C,3) = 0 1 1 ; 1 1 0 ; 1 0 1, menunjukkan adonan susunan dari any (C,1) dan any (C,2) tetapi peninjauan elemen benar atau salahnya di cari secara tersendiri bukan secara 'beberapa'
Pada matriks budi any bekerja pada :
- any (C) : beberapa dari elemen matriks C kolom 1, kolom 2, dan kolom 3 dari seluruh baris
- any (C,1) : beberapa dari elemen matriks C kolom 1, kolom 2, dan kolom 3 dari seluruh baris
- any (C,2) : beberapa dari elemen matriks C baris 1, baris 2, dan baris 3 dari seluruh kolom
- any (C,3) : pada semua elemen matriks C secara tersendiri
Dapat digambarkan sebagai berikut :

2. All

Matriks A didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi all dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- all (A) = 0, menunjukkan semua elemen larik A baris 1 seluruh kolom ialah bernilai salah (0) atau tidak benar (1)
- all (A,1) = 0 1 1, menunjukkan semua elemen larik A baris 1 kolom 1 bernilai salah (0), kolom 2 dan kolom 3 bernilai benar (1)
- all (A,2) = 0, menunjukkan semua elemen larik A baris 1 bernilai salah (0)
- all (A,3) = 0 1 1, menunjukkan semua elemen larik A baris 1 kolom 1 bernilai salah (0), kolom 2 dan kolom 3 bernilai benar (1)

Matriks B didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas
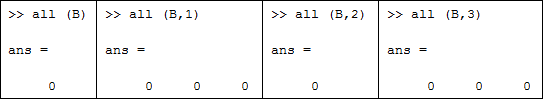
Kemudian dipakai budi all dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- all (B) = 0, menunjukkan semua elemen larik B baris 1 seluruh kolom ialah bernilai salah (0) atau tidak benar (1)
- all (B,1) = 0 0 0, menunjukkan semua elemen larik B baris 1 kolom 1, kolom 2, dan kolom 3 bernilai salah (0)
- all (B,2) = 0, menunjukkan semua elemen larik B baris 1 bernilai salah (0)
- all (B,3) = 0 0 0, menunjukkan semua elemen larik B baris 1 kolom 1, kolom 2, dan kolom 3 bernilai salah (0)

Matriks C didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi all dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- all (C) = 0 0 0, menunjukkan semua elemen matriks C kolom 1, kolom 2, dan kolom 3 bernilai salah (0) pada seluruh baris
- all (C,1) = 0 0 0, menunjukkan semua elemen matriks C kolom 1, kolom 2, dan kolom 3 bernilai salah (0) pada seluruh baris
- all (C,2) = 0 ; 0 ; 0, menunjukkan semua elemen matriks C baris 1, baris 2, dan baris 3 bernilai salah (0) pada seluruh kolom
- all (C,3) = 0 1 1 ; 1 1 0 ; 1 0 1, menunjukkan adonan susunan dari any (C,1) dan any (C,2) tetapi peninjauan elemen benar atau salahnya di cari secara tersendiri
Pada matriks budi all bekerja pada :
- all (C) : semua dari elemen matriks C kolom 1, kolom 2, dan kolom 3 dari seluruh baris
- all (C,1) : semua dari elemen matriks C kolom 1, kolom 2, dan kolom 3 dari seluruh baris
- all (C,2) : semua dari elemen matriks C baris 1, baris 2, dan baris 3 dari seluruh kolom
- all (C,3) : pada semua elemen matriks C secara tersendiri
Dapat digambarkan sebagai berikut :

3. Isempty

Matriks A, B, C, dan D didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi isempty dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- isempty : bernilai 1 kalau array memiliki himpunan yang kosong dan bernilai 1 kalau himpunan tidak kosong
4. Isnan

Matriks A dan C didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi isempty dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- isnan (is not a number) : bernilai 1 untuk nilai yang bukan angka misalnya ialah tak terhingga
5. Matriks Khusus

Matriks F didefinisikan berukuran 4x4 yang semua elemennya bernilai nol dengan algoritma 'zeros' untuk semua elemen bernilai nol dan '4' untuk dimensi matriks berukuran 4x4

Matriks G didefinisikan berukuran 3x3 yang semua elemennya bernilai satu dengan algoritma 'ones' untuk semua elemen bernilai satu dan '3' untuk dimensi matriks berukuran 3x3

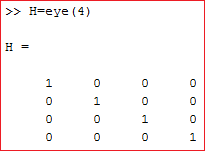
Matriks H didefinisikan berukuran 4x4 yang diagonal elemennya bernilai satu dengan algoritma 'eye' untuk diagonal elemen yang bernilai satu dan '4' untuk dimensi matriks berukuran 4x4
6. Matriks pada persamaan linier
2x - 3y + 5z = 20 .....(1)
x + z = -16 .....(2)
2y - 15z = 30 .....(3)
Persamaan linier diatas sanggup diselesaikan dengan metode matriks, yaitu :
a. Metode pembagian

Matriks k didefinisikan terlebih dahulu, yaitu koefisien dari x, y, dan z pada 3 persamaan linier diatas

Matriks l didefinisikan sebagai hasil dari 3 persamaan linier diatas (konstanta)

Matriks k lalu dibagi dengan matriks l dengan simbol '\' alasannya ialah secara teoritik ini ialah pembagian oleh invers
b. Metode determinan

Matriks k didefinisikan terlebih dahulu, yaitu koefisien dari x, y, dan z pada 3 persamaan linier diatas

Matriks l didefinisikan dari hasil 3 persamaan linier tersebut (konstanta) lalu dimasukkan pada kolom 1 baris 1, baris 2, dan baris 3 yang mana merupakan letak dari variabel x dari 3 persamaan linier tersebut

Matriks m didefinisikan dari hasil 3 persamaan linier tersebut (konstanta) lalu dimasukkan pada kolom 2 baris 1, baris 2, dan baris 3 yang mana merupakan letak dari variabel y dari 3 persamaan linier tersebut
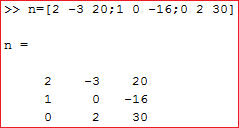
Matriks n didefinisikan dari hasil 3 persamaan linier tersebut (konstanta) lalu dimasukkan pada kolom 3 baris 1, baris 2, dan baris 3 yang mana merupakan letak dari variabel z dari 3 persamaan linier tersebut

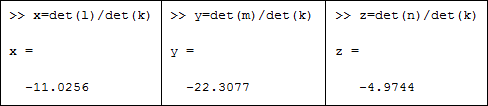
- Nilai x sanggup dicari dengan membagi matriks l dengan matriks k memakai simbol '/' alasannya ialah pembagian biasa
- Nilai y sanggup dicari dengan membagi matriks m dengan matriks k memakai simbol '/' alasannya ialah pembagian biasa
- Nilai z sanggup dicari dengan membagi matriks n dengan matriks k memakai simbol '/' alasannya ialah pembagian biasa
7. Magic

Logika magic dipakai untuk membentuk matriks berukuran NxN dan penjumlahan tiap baris per baris, kolom per kolom, dan diagonal per diagonal ialah sama, perhitungan dimulai dari 1 hingga N2.
Misal N=4 maka matriks yang terbentuk ialah matriks ukuran 4x4 dan nilai dari 1 hingga 42 = 16. Penjumlahan baris per baris, kolom per kolom, dan diagonal per diagonal 34

Nilai N = 3 dan nilai yang dihitung ialah dari 1 hingga 32 = 9. Penjumlahan baris per baris, kolom per kolom, dan diagonal per diagonal 15
8. Diag

Larik v didefinisikan terlebih dahulu pada Command Window dan karenanya menyerupai gambar diatas

Kemudian dipakai budi diag dan karenanya menyerupai gambar diatas. Berdasarkan hasil percobaan tersebut sanggup disimpulkan :
- diag : mengubah elemen-elemen pada array menjadi elemen-elemen matriks diagonal sesuai dengan banyaknya baris atau kolom pada array

diag(v,1) berfungsi untuk mengubah elemen-elemen pada array menjadi elemen-elemen matriks diagonal yang diagonalnya naik keatas atau naik 1 tingkat dari diagonal awal

diag(v,-1) berfungsi untuk mengubah elemen-elemen pada array menjadi elemen-elemen matriks diagonal yang diagonalnya turun kebawah atau turun 1 tingkat dari diagonal awal
9. Triu dan Tril

x didefinisikan terlebih dahulu pada Command Window sebagai magic (5) dan karenanya menyerupai gambar diatas

Logika triu dipakai pada variabel x sehingga nilai dibawah diagonal tengah bernilai nol.
Makara budi trius dipakai untuk menciptakan nol nilai dibawah diagonal tengah dari suatu matriks

Logika tril dipakai pada variabel x sehingga nilai diatas diagonal tengah bernilai nol.
Makara budi triul dipakai untuk menciptakan nol nilai diatas diagonal tengah dari suatu matriks
Belum ada Komentar untuk "Laporan Praktikum Larik Dan Matrik 3"
Posting Komentar